摘要
- Introduction
- 工作流程:Forward-Propagation、Backward Propagation、Partial Derivatives、Hyper Parameters
- 深度网络:A single layer Neural Network、Wide Neural Network vs Deep Neural Network
- 维度诅咒、权衡

Introduction
神经网络试图复制人脑的工作以使事情更加智能化。
神经网络通常是一种有监督的学习方法。这意味着需要有一套训练集。理想情况下,训练集合包含了绝对真值(tags | 标签,classes | 类 )的例子。例如在文本情感分析的情况下,训练集是句子列表和它们各自对应的情绪。(注意:未标记的数据集也可以用来训练神经网络,但这里仅考虑最基本的情况。)
例如:将文本称为 X ,将它们的标签称为 Y 。 有一些函数可以定义 X 和 Y 之间的关系,比如是什么特征(词/短语/句子结构等)导致一个句子是否定的或肯定的的含义。早期的人们习惯于手动查找这些特征,这被称为特征工程(feature engineering)。神经网络使得这一过程实现自动化处理。
So there are many ways you can understand a concept, choose whichever suits you, being persistent about the learning part. At the end knowing maths is a useful tool when it comes to optimisations or experimentations.
工作流程
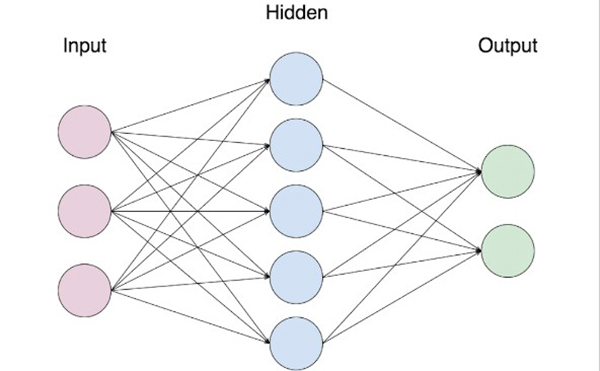
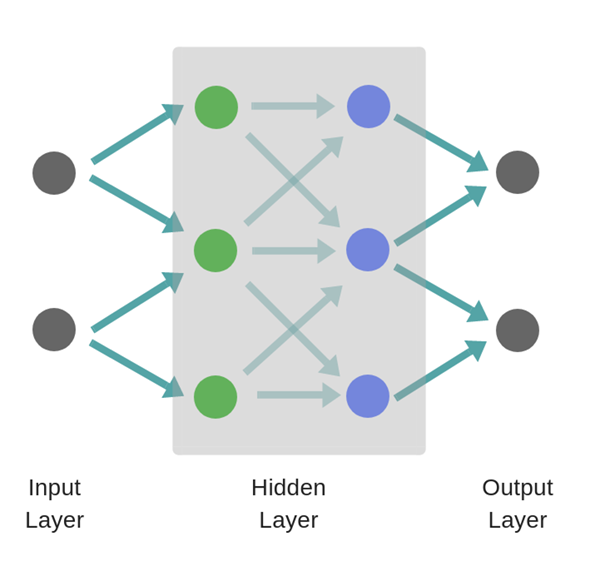
人工神经网络由3个组成部分组成:
- 输入层 Input Layer
- 隐藏(计算)层 Hidden (computation) Layers
- 输出层 Output Layer
学习过程分两步进行:
- 前向传播 Forward-Propagation:猜测答案
- 反向传播 Back-Propagation:最小化实际答案和猜测答案之间的误差
前向传播 Forward-Propagation
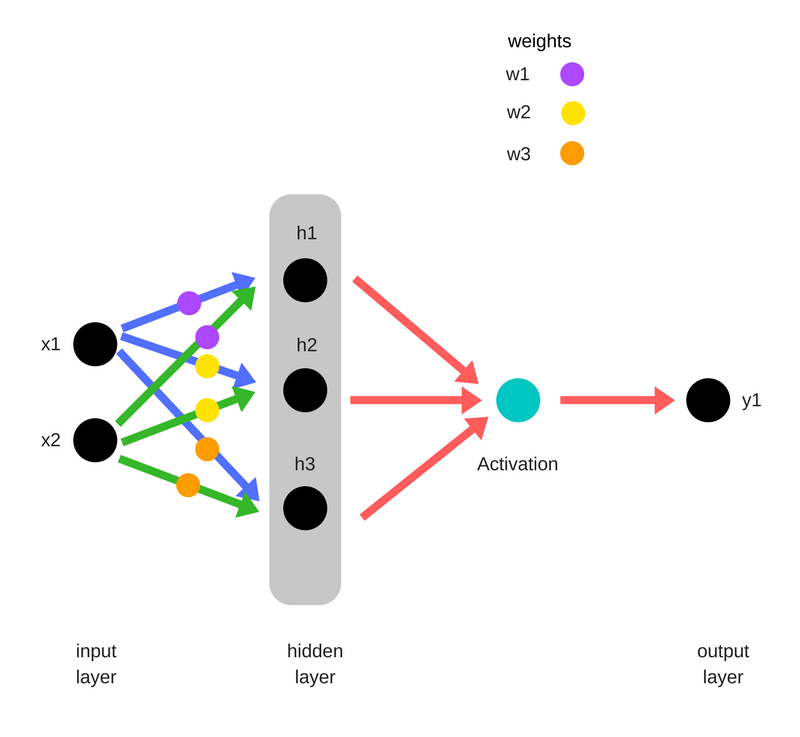
随机初始化权重(Randomly initialize weights)
- w1
- w2
- w3
输入层的数据乘以权重形成隐藏层 - h1 = (x1 * w1) + (x2 * w1)
- h2 = (x1 * w2) + (x2 * w2)
- h3 = (x1 * w3) + (x2 * w3)
隐藏层的输出通过非线性函数(激活函数)以形成猜测输出(guessed output) - y_ = fn( h1 , h2, h3 )
反向传播 Backward Propagation

- 总误差 total_error 通过一个代价函数 (cost function) 来计算,参数为计算期望值( expected value ) y(训练集中的值)和观测值(observed value) y_(前向传播值)
- 按每一个权重计算误差的偏导数(这些偏微分是每一个权重在总误差中的量度)
- 微分后乘以一个小数 ( η ) ,η 称为学习率(learning rate)
- 然后从各自的权重中减去结果
反向传播的结果是以下更新的权重:
- w1 = w1 - (η * ∂(err) / ∂(w1))
- w2 = w2 - (η * ∂(err) / ∂(w2))
- w3 = w3 - (η * ∂(err) / ∂(w3))
基本上我们对权重初始化时是随机的,并假设他们会产生准确的答案。
Those familiar with Taylor Series, backpropogation shares the same end result with it. But instead of an indefinite series we try to optimise the first element only.
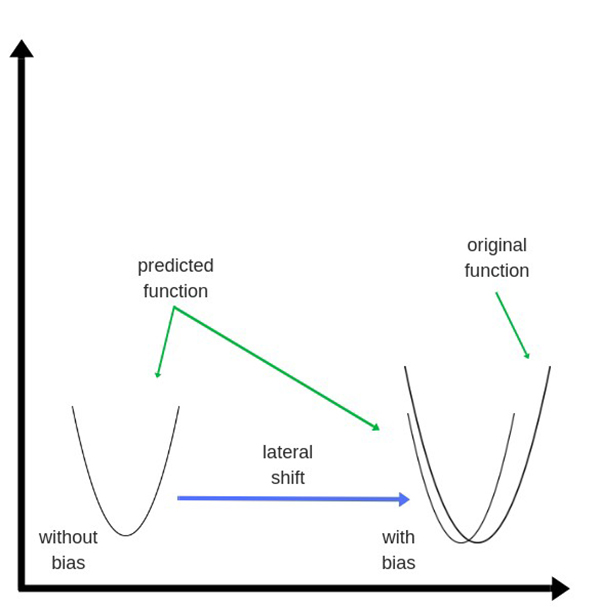
偏差(Bias)是添加到隐藏层的权重。它们也被随机初始化并以隐藏层相似的方式更新。虽然隐藏层的作用是映射数据中底层函数(underlying function)的模型,但偏差的作用是横向移动学习函数(the learned function),使其与原始函数(the original function)重叠。
偏导数 Partial Derivatives
计算偏导数使我们能够知道每个权重对误差的贡献。
导数的需求是显而易见的。例如:假设一个试图找到自动驾驶汽车最佳速度的神经网络。现在,如果汽车发现速度比预期的更快或者更慢,那么神经网络会通过加速或减速来改变速度。什么是加速/减速?速度的导数。
解释偏导数:射飞镖
假设有几个孩子被要求向飞镖靶掷飞镖,瞄准中心。最初的结果是:
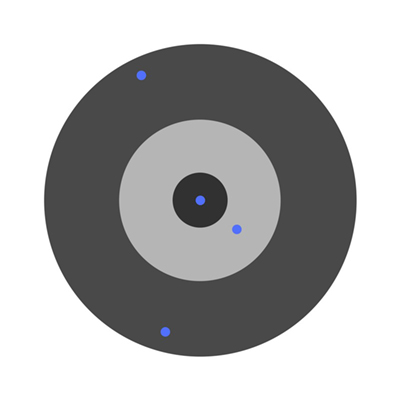
现在如果我们确认了总误差并简单地从所有权重中减去,那么我们可以概括每个学生的误差。假设一个孩子瞄准的目标太低,但是我们要求所有的孩子都瞄准得更高一些,结果是:
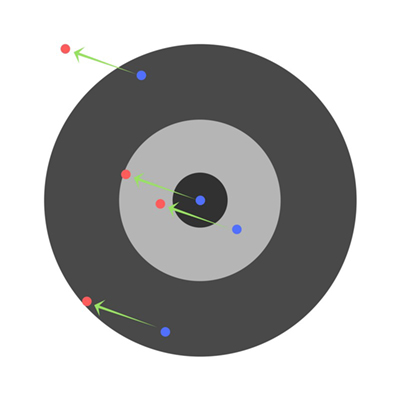
一些学生的错误可能会减少,但总体错误仍然会增加。通过查找偏导数,我们可以找出每个权重单独产生的误差。单独修正每个权重会得到以下结果:
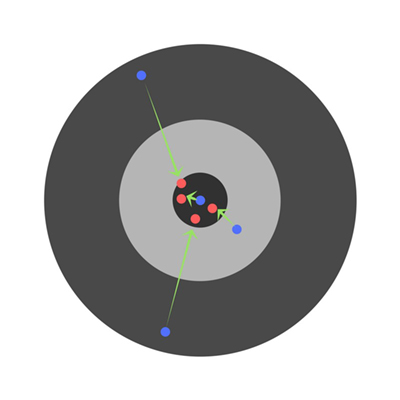
超参数 Hyper Parameters
虽然神经网络被用于自动化特征选择,但是仍然有一些参数我们必须手动输入。
学习速率 Learning Rate
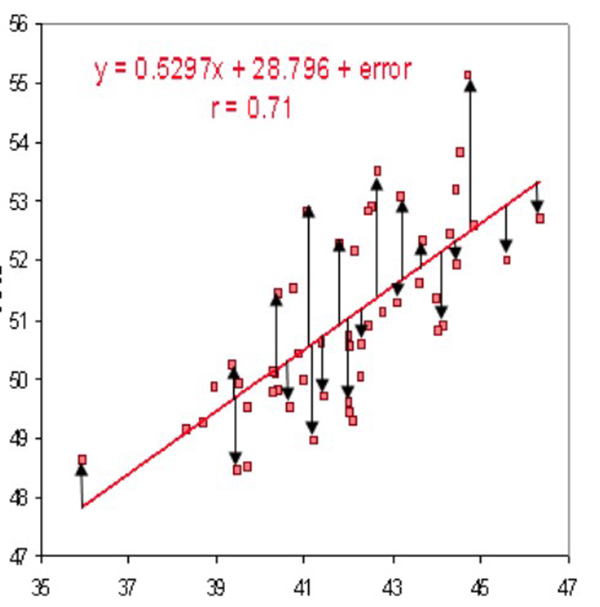
学习速率是一个非常关键的超参数。如果学习速率太小,那么即使在长时间训练神经网络之后,它仍将远离最优结果。结果看起来像:
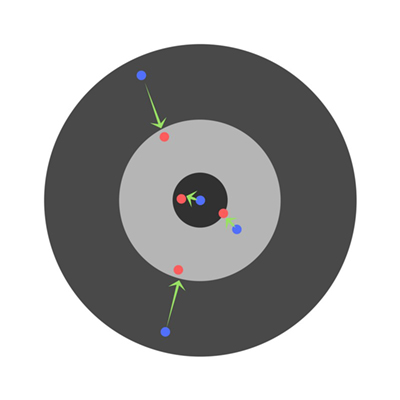
相反,如果学习率太高,那么学习者就会过早地得出结论。产生以下结果:
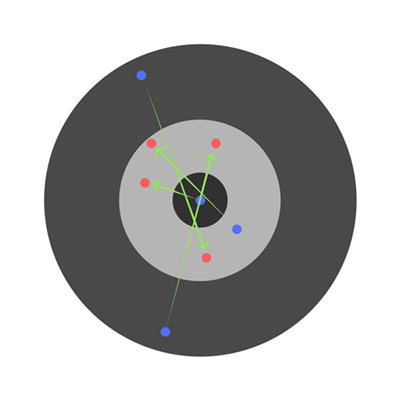
激活函数 Activation Function
简单来说,激活函数(激励函数)负责决定哪些神经元将被激活,即什么信息将传递给其他层。没有激活函数,深度神经网络将失去大量的描述学习能力。
这些函数的非线性负责增加学习者的自由度,使他们能够在较低维度上推广高维的问题。
下面是一些流行的激活函数的例子: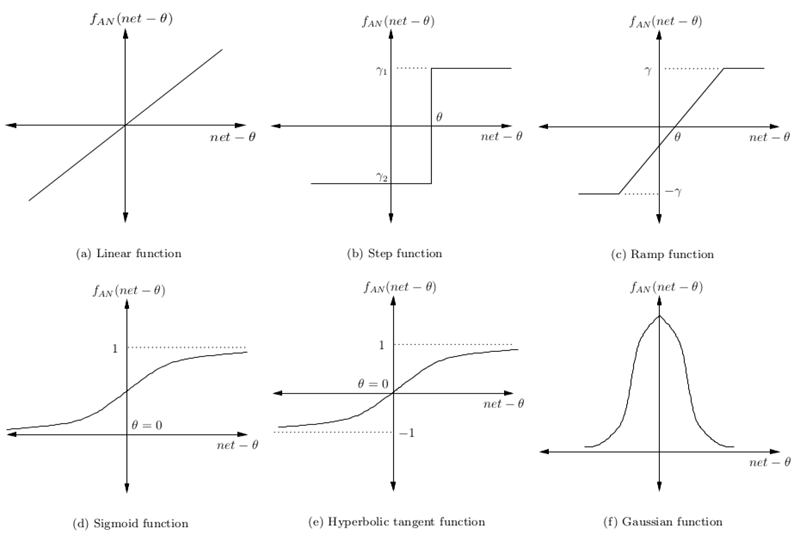
成本函数 Cost Function
成本函数是神经网络的核心。它用于计算真实和观察结果的损失(loss)。我们的目标是尽量减少这种损失。因此,成本函数有效地推动了神经网络对其目标的学习。
成本函数是神经网络做的“有多好”的量度,在给定训练样本和预期输出方面。它也可能取决于变量,如权重(weights)和偏差(biases)。
成本函数是一个单一的值,而不是一个矢量,因为它评价了神经网络作为一个整体的效果。
一些最着名的成本函数是:
- 平方平均数 Quadratic Cost ,简称均方根 Root Mean Square
- 交叉熵 Cross Entropy
- 指数 Exponential (AdaBoost)
- 相对熵 Kullback–Leibler divergence 或者 信息收益 Information Gain
均方根是其中最简单和最常用的。它被简单地定义为:
Loss = √(expected_output ** 2) - (real_output ** 2)
神经网络中的成本函数应满足两个条件:
- 成本函数必须能够写成平均值
- 成本函数不能取决于除一个神经网络中的输出值以外的的任何激活值
深度网络
深度学习是一类机器学习算法,可以从数据中学习更深入(更抽象)的洞察力。
- 使用级联,类似流水线的依次传递管道,拥有多层处理单元(非线性)进行特征提取和转换。
- 基于以无监督方式学习数据的特征(表示数据知识)。更高级别的特征(在后面的处理图层中找到)是从更低级别的特征(可在初始处理图层中找到)导出的。
- 多级表示相对应的不同抽象级别;这些级别构成了概念的层次结构。
单层神经网络 A single layer Neural Network
单层神经网络,无论第一层(绿色神经元)如何学习,他们只需将其传递给输出即可。

双层神经网络 Two layer Neural Network
对于两层神经网络,无论绿色隐藏层学习什么,都要传递到蓝色隐藏层,进一步学习(关于绿色层学习)。因此,隐藏层的数量越多,对先前已经学习过的概念的学习就越多。
Wide Neural Network vs Deep Neural Network
在一层中存在更多神经元的情况下,它不会获得更深层次的洞察力。相反,它的结果是学习到更多的概念。
例:学习英语语法,它需要理解大量的概念。在这种情况下,单层宽神经网络比深度神经网络的效果要好得多,而深度神经网络的宽度要小得多。

但在学习傅立叶变换(Fourier Transform)的情况下,学习者(神经网络)需要深入学习,因为没有太多的概念需要学习,但每个概念都足够复杂,需要深度学习。
Balance is Key
每个任务都使用深度和宽度神经网络是非常诱人的。这可能是一个非常糟糕的主意,因为:
- 两者都显然需要更多的数据才能达到最低的理想精度(desirable accuracy)
- 两者都具有成倍增加的时间复杂度(time complexity)
- 太深的神经网络将尝试更深入地分解一个基本概念,但在这一点上它将对这个概念做出错误的假设,并试图找到不存在的伪模式(pseudo patterns)
- 太宽的神经网络会试图找到更多数量的特征(可测量特性)。因此,与上面类似,它将开始对数据做出错误的假设。
维度诅咒
维度诅咒(The curse of dimensionality)是指在高维空间(通常具有数百或数千维度)中分析和组织数据时出现的各种现象,这些现象在低维设置中不会发生。
像英语语法或股票奖品等有很多影响他们的特征。使用机器学习必须用具有有限和相对小得多的长度(比实际存在的特征的数量)的阵列(array)/ 矩阵(matrix)来表示这些特征。要做到这一点可能产生两个问题:
- made by a learner:由于学习者的错误假设而出现偏差。高偏差会导致算法错过功能与目标输出之间的相关关系。这种现象被称为欠拟合(underfitting)。
- insufficient learning : 由于对特征的了解不全面,训练集中的小波动导致较大偏差。高方差导致过度拟合(overfitting),将错误作为相关信息进行学习。
权衡
It is typically impossible to have low bias and low variance.
在训练早期因为网络输出远未达到要求,偏差很大。由于数据影响较小,方差很小。在训练后期因为网络已经学会了潜在的功能,偏差很小。
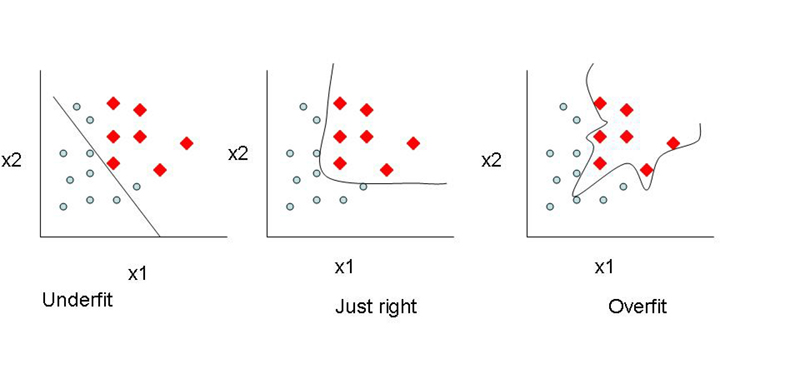
然而,如果训练太长,网络也将学习该数据集特殊的噪声。这导致在不同数据集上测试的结果表现为高方差,因为不同数据集的噪声存在变化。实际上,具有高偏差的算法通常产生更简单的模型,这些模型不倾向于过度拟合,但可能会削弱其训练数据,而不能捕获重要的模式或特征的属性。具有低偏差和高方差的模型在结构上通常更复杂,使得它们能够更准确地表示训练集。然而,在这一过程中,它们也可能代表训练集中的占比较大的噪声,使得它们的预测尽管复杂性增加,但精度却不太精确。
因此,低偏差和低方差同时存在通常是不可能的。
目前,依靠丰富的数据和工具,我们可以轻松地创建复杂的机器学习模型。如果学习者没有提供足够的信息时,实际上偏差就发生了,处理过度拟合将变成中心工作。如果提供更多的例子,则意味着更多的变化,包括模式的数量都增加了。
扩展阅读
《The Machine Learning Master》

- Machine Learning(一):基于 TensorFlow 实现宠物血统智能识别
- Machine Learning(二):宠物智能识别之 Using OpenCV with Node.js
- Machine Learning:机器学习项目
- Machine Learning:机器学习算法
- Machine Learning:如何选择机器学习算法
- Machine Learning:神经网络基础
- Machine Learning:机器学习书单
- Machine Learning:人工智能媒体报道集
- Machine Learning:机器学习技术与知识产权法
- Machine Learning:经济学家谈人工智能
- 数据可视化(三)基于 Graphviz 实现程序化绘图
